Why is Inverse Sinx Continuous and Differentiable
The Derivative of Trig Functions
The limit of sin x / x as x goes to 0
In a few minutes, we will find it important to know what
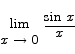
is. Here is a graph of the function near 0.
The plot suggests that the limit should be 1. How do we go about proving that this is true?
The function that we are taking the limit of suffers a 0/0 problem. Up to this point, we have been handling 0/0 problems by doing to algebra with an aim toward factoring out common terms that cause the 0/0 problem and then cancelling them away. Unfortunately, that option is not open to us here. Instead, our strategy will be based on the squeeze theorem.
The squeeze theorem
Let g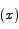 and
and 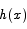 be two functions that both converge to the same limit:
be two functions that both converge to the same limit:
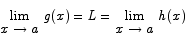
If 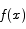 is a function that satisfies
is a function that satisfies
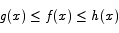
for all x, then
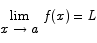
Proving the sin x / x limit
The proof that the limit of sin x/x as x approaches 0 is 1 will make use of the squeeze theorem. Specifically, we are going to compare three areas that depend on x and watch what happens to these areas as x goes to 0. The picture below shows the three areas inscribed in a circle of radius 1.
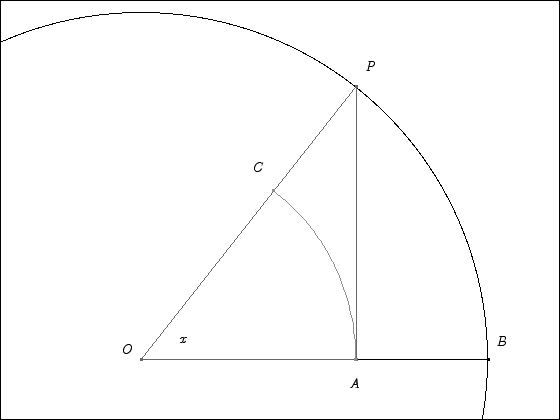
The first and smallest region is the pie-shaped sector bounded by the points A, O, and C. The middle region is the triangle bounded by the points A, O, and P. The outer region is the pie-shaped sector bounded by the points B, O, and P. It is obvious from the picture that regardless what the value of the angle x is we have
| area of sector OAC < area of triangle OAP < area of sector OBP | (1) |
Next, we need to determine the areas of these regions as a function of x. To compute the areas of the two sectors we can use a proportionality argument: since the area of an entire circle with radius r is 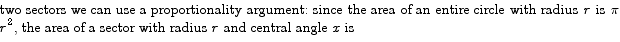 , the area of a sector with radius r and central angle x is
, the area of a sector with radius r and central angle x is
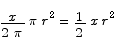
because the sector represents a fraction 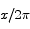 of the area of the entire circle.
of the area of the entire circle.
To compute the area of the sector OAC, we need to know the radius of that sector. That radius is given by the length of the line from O to A. We can use some simple trig to figure out that length, as the picture below shows.
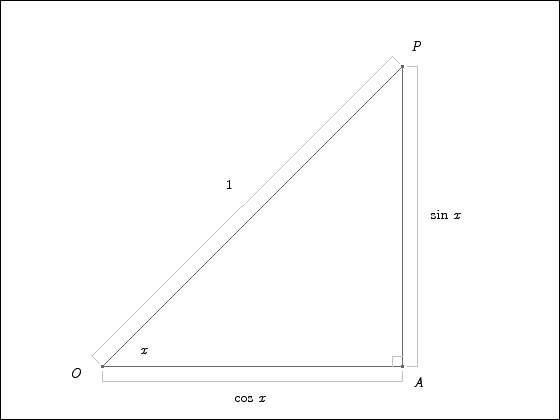
Since the hypotenuse of the triangle OAC has length 1, the length of the side OA is cos x. Thus
| | (2) |
We can determine the area of the triangle OAP as follows:
| | (3) |
Since the outer sector has radius 1 and central angle x, we have
| | (4) |
Putting inequality (1) together with equations (2), (3), and (4) produces
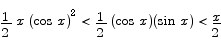
Recall that we are interested in the value of sin x/x. To make that quantity appear in the middle expression, we divide through by 1/2 x cos x. The result is
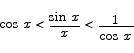
Finally, if we use the fact that
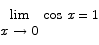
which leads to
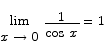
We get
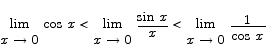
and by the squeeze theorem we have
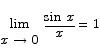
The limit of (1 - cos x)/x as x goes to 0
A closely related problem that can be solved by a similar technique is
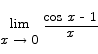
The text gives a very slick proof that this limit is 0:
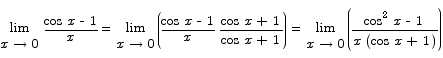
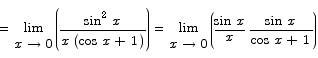
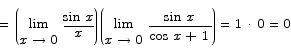
Alternative Geometric Proof
If you would prefer a more geometric proof that this limit is 0, here it is. To start with, we draw a figure that the proof will be based on.
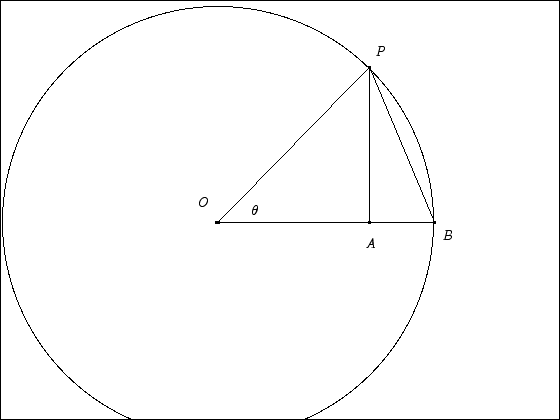
The circle has a radius of 1, and the angle POA is  . The proof is based on the ratio
. The proof is based on the ratio
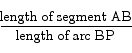
and the behavior of that ratio as the angle  goes to 0. The first thing to note is that since both distances are positive, the ratio will be greater than 0. If you work out the lengths of these two things you discover that
goes to 0. The first thing to note is that since both distances are positive, the ratio will be greater than 0. If you work out the lengths of these two things you discover that
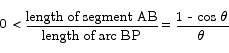
which is precisely the quantity we are interested in. The next step is to replace the length of the arc from B to P with the length of the line segment from B to P. Since the line segment will always be shorter than the arc, making this switch will increase the value of the fraction overall. We have
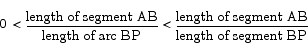
The next thing to do is to figure out the lengths of the two segments in the fraction to the right. We already know that

All that remains is to figure out what the length of segment BP is. For this, we draw a more detailed picture of the triangle OBP.
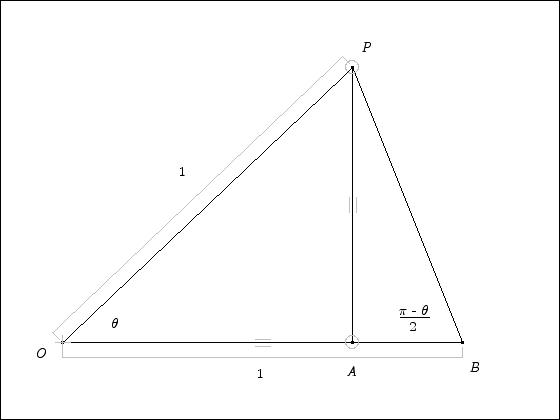
Since the triangle OBP is an isoceles triangle (sides OB and OP both have length 1), we can see that the angles at B and P have to be the same. Since the angles have to add up to 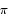 , we have
, we have
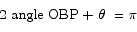
or
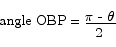
Now, look at the ratio we need to understand:
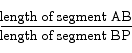
Once we know the angle OBP we can use the fact that the triangle ABP is a right triangle to see
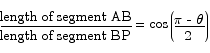
Thus we have that
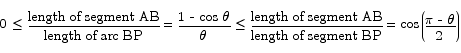
In the limit as  goes to 0 we see that the term all the way to the right goes to 0. Since the thing we are interested in is trapped between two things that both go to zero, it must also go to 0.
goes to 0 we see that the term all the way to the right goes to 0. Since the thing we are interested in is trapped between two things that both go to zero, it must also go to 0.
The Derivatives of sin x and cos x
We can use the definition of the derivative to compute the derivatives of the elementary trig functions.
Theorem The function sin x is differentiable everywhere, and its derivative is cos x.
Proof Once again, we work from the definition.
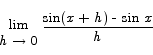
The only manipulation that suggests itself readily is to use the addition formula for sine to expand the sin(x+h) term.
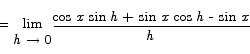
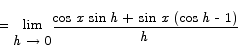
The latter breaks up naturally into limits we can compute.
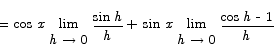
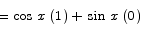
= cos x
You can further convince yourself that the derivative of sine is cosine by looking at a picture of the two functions plotted side by side. At each point, the slope of the curve sin x is given by the derivative, namely cos x. Indeed, you can see that when sin x has zero slope cosine has value 0, and so on.
Similar methods will get us
Theorem The function cos x is differentiable everywhere, and its derivative is -sin x.
Proof From the definition we have
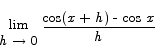
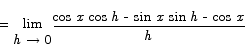
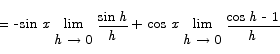
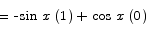
= -sin x
Derivatives of other trig functions
We could proceed to compute the derivatives of all of the other trig functions from the definition of the derivative, but there is no reason to work so hard. Since every other trig function can be expressed as a combination of sine and cosine, we can combine the last two results with the differentiation rules we developed last time.
For example, to compute the derivative of the tangent, we compute
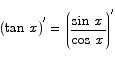
We apply the quotient rule
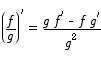
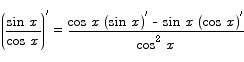
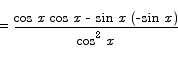
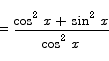
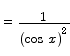
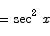
Homework
Section 3.4: 3, 4, 9, 10, 18, 30, 33, 46
Source: https://www2.lawrence.edu/fast/GREGGJ/Math140/043/043TrigDerivatives.html
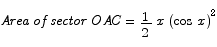
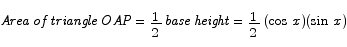
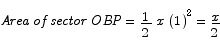
0 Response to "Why is Inverse Sinx Continuous and Differentiable"
Post a Comment